Menu
Johann Carl Friedrich Gauss (30 April 1777 Braunschweig – 23 February 1855 Göttingen) was a German mathematician who contributed significantly to many fields, including number theory, algebra, statistics, analysis, differential geometry, geodesy, geophysics, mechanics, electrostatics, astronomy, matrix theory, and optics.
Among the many scientific fields that Gauss has made major contributions to, we focus here on his contribution to statistics and estimates. Before describing that part of his work, let's first take a look at his early years.
Johann Carl Friedrich Gauss was born in Brunswick (Braunschweig), in the Duchy of Brunswick-Wolfenbüttel (now part of Lower Saxony, Germany), as the son of poor working-class parents. His mother was illiterate and never recorded the date of his birth, remembering only that he had been born on a Wednesday, eight days before the Feast of the Ascension, which itself occurs 39 days after Easter. Gauss later solved this puzzle about his birthdate in the context of finding the date of Easter, deriving methods to compute the date in both past and future years.
Gauss was a child prodigy. A contested story relates that, when he was eight, he figured out how to add up all the numbers from 1 to 100. There are many other anecdotes about his precocity while a toddler, and he made his first ground-breaking mathematical discoveries while still a teenager. He completed Disquisitiones Arithmeticae, his magnum opus, in 1798 at the age of 21, though it was not published until 1801. This work was fundamental in consolidating number theory as a discipline and has shaped the field to the present day. Gauss's intellectual abilities attracted the attention of the Duke of Brunswick, who sent him to the Collegium Carolinum (now Braunschweig University of Technology), which he attended from 1792 to 1795, and to the University of Göttingen from 1795 to 1798. While at university, Gauss independently rediscovered several important theorems.
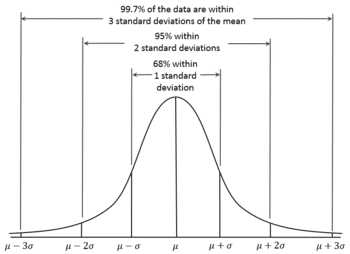The name 'Gauss' could bring back memories of our high-school mathematics lessons about 'normal distributions'. In 1809, Gauss developed the formula for the normal distribution and showed that errors were fit well by this distribution. In general, Gauss's contributions to statistics may be classed under the general heading of least squares, although this gives little indication of their scope or impact. His first exposition of least squares was given in 1809 when he was 31, but these ideas must have been formulated much earlier, apparently first when he was 17. In Book 2, Section 3 of his book on planetary orbits, he discussed the estimation of the six constants or parameters that determine the elliptical orbit on the basis of n > 6 observations. He began it in article 175 with:
"To this end let us leave our special problem, and enter upon a very general discussion and one of the most fruitful in every application of the calculus to natural philosophy".
His second exposition was presented in a series of three lengthy papers to the Royal Society of Göttingen. Here he introduced the subject as follows
"The problem is certainly the most important which the application of mathematics to natural philosophy presents".
In spite of the importance he obviously attributed to the subject, as evidenced by the above quotations, he appeared not to have returned to it in later years, at least in print, although he continued lecturing on it.
It is important to note here that Adrien-Marie Legendre published the first description of the metho, in 1805, and was responsible for the name "least squares". However, it was Gauss, not Legendre, who developed the method into a statistical tool, embedding it into a statistical framework, involving the probabilistic treatment of observational errors, and thus set the famous linear model on its modern course. For example, consider the following quotations from Fisher:
"Gauss, moreover, approached the problem of statistical estimation in an empirical spirit, raising the
question of the estimation not only of probabilities, but of other quantitative parameters. He perceived the aptness for this purpose of the Method of Maximum Likelihood, although he attempted to derive and justify this method from the principle of inverse probability... Gauss, further, perfected the systematic fitting of regression formulae, simple and multiple, by the method of least squares..."
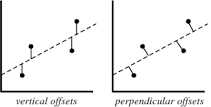The least squares method is a form of mathematical regression analysis that finds the line of best fit for a dataset, providing a visual demonstration of the relationship between the data points. Public Health relies heavily on measurements of diseases and their determinants within populations. Such measurements are often prone to various degrees of error. Public Health Scientists use mathematics to describe relationships between their measurements of determinants (risk factors, protective factors) and their measurements of disease. The Least Squares Method helps them to find the best fitting relation (usually a line) in their data. Gauss has given us a tool to describe those relations, which helps us to understand how factors influence the risk of disease.